Kreuzprodukt von Vektoren

In dieser Veröffentlichung werden wir uns überlegen, wie man das Kreuzprodukt zweier Vektoren findet, eine geometrische Interpretation, eine algebraische Formel und Eigenschaften dieser Aktion geben und auch ein Beispiel zur Lösung des Problems analysieren.

Geometrische Deutung

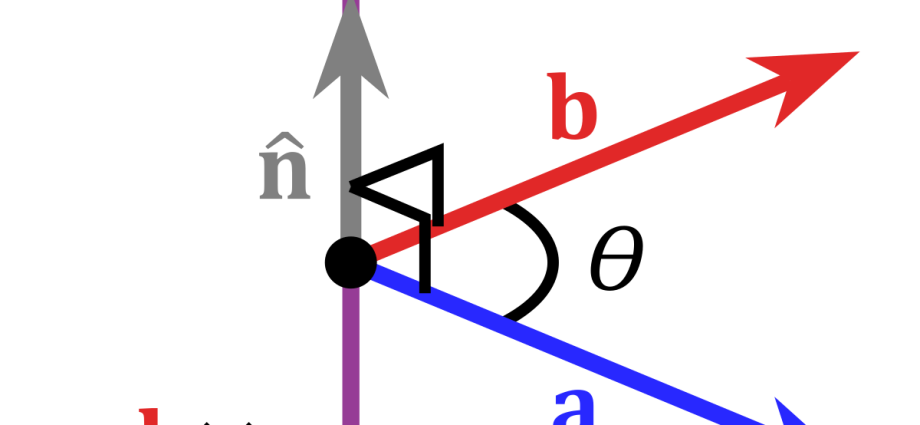
Vektorprodukt zweier Nicht-Null-Vektoren a и b ist ein Vektor c, was als bezeichnet wird [a, b] or a x b.

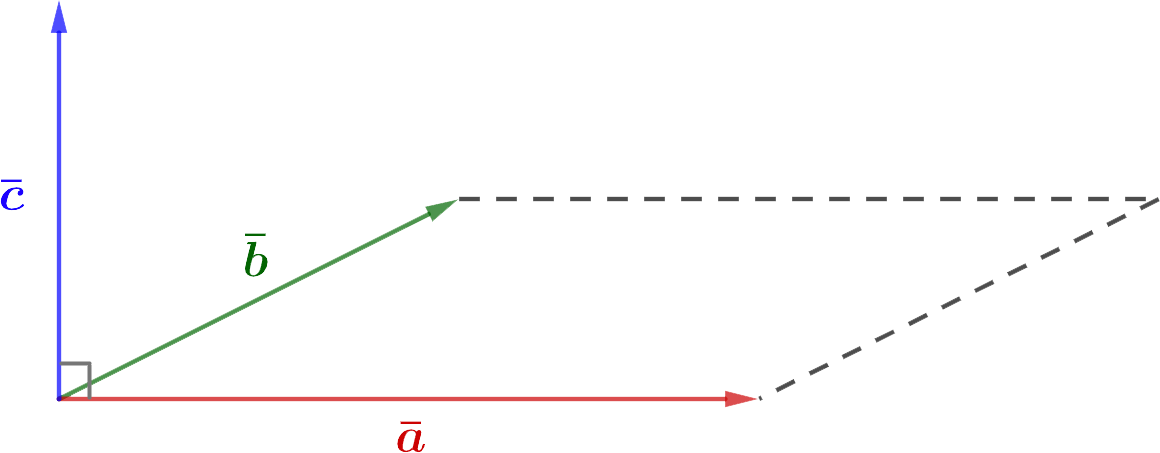
Vektorlänge c ist gleich der Fläche des aus den Vektoren konstruierten Parallelogramms a и b.

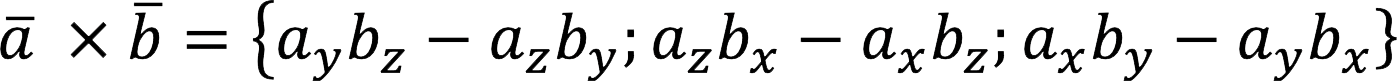
In diesem Fall c senkrecht zu der Ebene, in der sie sich befinden a и b, und ist so angeordnet, dass die geringste Drehung aus a к b gegen den Uhrzeigersinn (aus Sicht des Vektorendes) durchgeführt.

Cross-Produkt-Formel

Produkt von Vektoren a = {ein_x;; zu_y,_z} ich b = {b_x;; b_y, B_z} wird mit einer der folgenden Formeln berechnet:

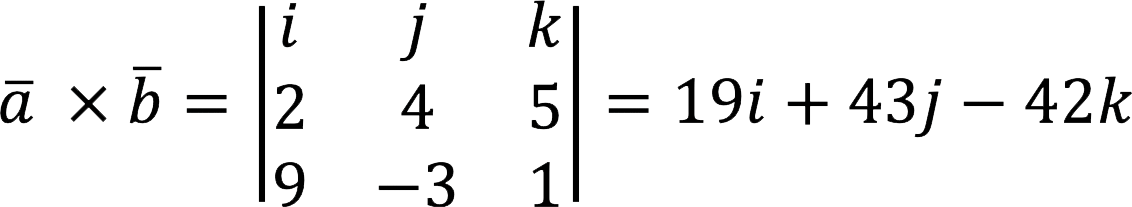
Produktübergreifende Eigenschaften

1. Das Kreuzprodukt zweier Vektoren ungleich Null ist genau dann gleich Null, wenn diese Vektoren kollinear sind.

[a, b] = 0Wenn a || b.

2. Der Modul des Kreuzprodukts zweier Vektoren ist gleich der Fläche des von diesen Vektoren gebildeten Parallelogramms.

S_Parallel = |a x b|

3. Die Fläche eines Dreiecks, das von zwei Vektoren gebildet wird, ist gleich der Hälfte ihres Vektorprodukts.

S_Δ = ¹/₂ · |a x b|

4. Ein Vektor, der ein Kreuzprodukt zweier anderer Vektoren ist, steht senkrecht zu ihnen.

c ⟂ a, c ⟂ b.

5. a x b = -b x a

6. (M a)X a = a x (M b) = m (a x b)

7. (a + b)X c = a x c + b x c

Beispiel für ein Problem

Berechnen Sie das Kreuzprodukt a = {2; 4; 5} и b = {9; -zwei; 3}.

Entscheidung:

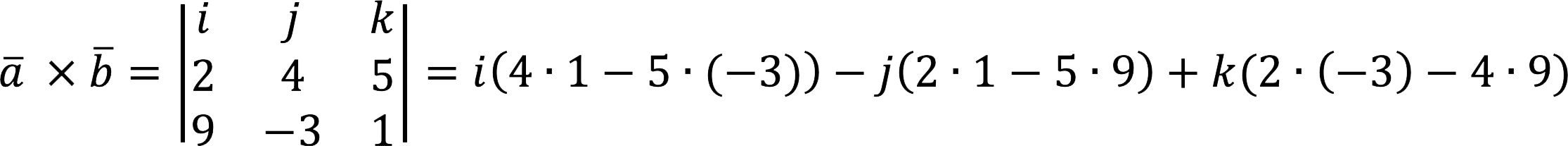
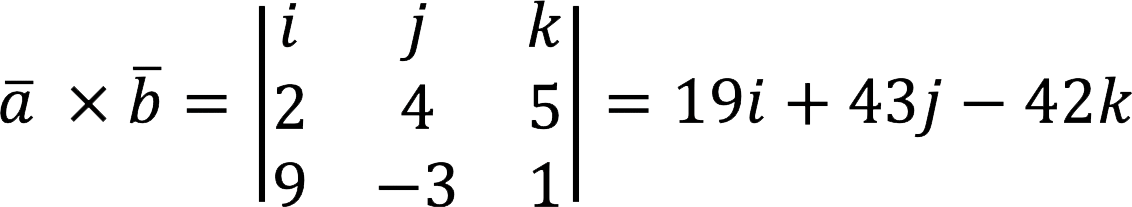
Antworten: a x b = {19; 43; -42}.